FIDO2 - Passwortlose Authentifizierung
Die fido Alliance möchte mit dem FIDO2 Standard nicht weniger, als die Art, wie wir uns in unserem digitalen Alltag authentifizieren, zu revolutionieren. Versprochen wird eine einfach zu handhabende Lösung, die Passwörter, auf lange Sicht, vollkommen ablöst und dabei deutlich sicherer ist als herkömmliche Authentifizierungslösungen. An den meisten Leuten, die nicht den neuesten Tech-Trends folgen, dürft FIDO2 jedoch bisher unbemerkt vorbeigezogen sein. Wenn überhaupt, ist der Begriff YubiKey bekannt, bei welchem es sich wohl um den geläufigsten FIDO2 Authenticator handelt.

In diesem Beitrag wollen wir FIDO2 etwas näher betrachten und den Unterschied zu klassischer Authentifizierung, mittels Passwort, aufzeigen.
Der Status quo
Je nachdem wie ausgeprägt unser digitales Leben ist, besitzen wir Konten bei 100 bis 200 Unternehmen, darunter Google, Microsoft, DB und viele weitere. Die Authentifizierungsstrategie bei jedem einzelnen dieser Accounts ist mit hoher Wahrscheinlichkeit, Multifaktorauthentifizierung kurz ausgeklammert, der Login mittels E-Mail und Passwort.
Bei Passwörtern handelt es sich um eine geheime Folge aus Buchstaben, Zahlen und Symbolen, von der nur wir Kenntnis besitzen (Faktor Wissen). Beim Login überprüft die jeweilige Anwendung, ob wir im Besitz des nötigen Wissens (Passwort) sind, indem wir das Passwort an die Anwendung übermitteln. Ist das übermittelte Geheimnis korrekt, so haben wir uns erfolgreich authentifiziert und können zum Beispiel die nächste Fahrt mit der Bahn buchen oder eine Zahlung tätigen.
Leider ist diese Authentifizierungsmethode extrem anfällig für Angriffe, bei denen entweder alle möglichen Passwörter durchprobiert werden (Brute Forcing) bis das richtige dabei war oder es wird sich nur auf die gängigsten Passwörter konzentriert, in der Hoffnung das dieses vom jeweiligen Nutzer ebenfalls verwendet wird (Dictionary Attack).
Aus diesem Grund empfiehlt die OWASP eine Passwortlänge von mindestens 8 Zeichen, wobei das Passwort aus einer willkürlichen Kombination aus Buchstaben, Zahlen und Sonderzeichen bestehen sollte.
Menschen sind leider nicht dafür konzipiert, sich solche komplexen Passwörter zu merken und erschwerend kommt hinzu, dass empfohlen wird für jeden Account ein anderes Passwort zu verwenden. Dies führt dazu, dass viele Menschen zu schwache Passwörter verwenden, auch wenn Lösungen wie Passwortmanager existieren.
Ein weiteres großes Risiko sind sogenannte Datenpannen, bei denen Angreifer unerlaubter weise Datenbanken auslesen und so unter anderem an die Passwort-Hashes der Nutzer kommen. Diese können im Anschluss gebrochen werden. Besonders beliebt sind dabei Rainbow-Tables, bei denen Tabellen mit vorberechneten Klartext-Hashvalue-Paaren zum Einsatz kommen.
Details wie etwa Salts wurden unterschlagen um einen groben Rahmen zu skizzieren.
FIDO2 Basics
FIDO2 geht einen anderen Weg, indem statt einem Geheimnis sogenannte digitale Signaturen zum Einsatz kommen. Um zu verstehen was das bedeutet, müssen wir uns aber erst mit etwas Mathematik und der Definition von Kryptosystemen beschäftigen.
Kryptosysteme
Kryptosysteme sind definiert als Fünf-Tupel (P, C, K, enc, dec) und können dazu verwendet werden um Daten zu ver- und entschlüsseln.
- $P$ ist der Plaintext-Space. Hierbei handelt es sich um die Menge aller möglichen Klartexte, die verschlüsselt werden können.
- $C$ ist der Ciphertext-Space. Hierbei handelt es sich um die Menge aller möglichen Ciphertexte, die aus der Verschlüsselung des jeweils zugehörigen Klartexts resultieren.
- $K$ ist der Schlüsselraum. Hierbei handelt es sich um die Menge aller möglichen Schlüssel, mit ver- bzw. entschlüsselt werden kann. Jeder Schlüssel definiert in Kombination
encbzw.deceine eindeutige Relation zwischen Klartext- und Ciphertextraum, d.h. für ein festes $k \in K$ bildet ein $x \in P$ genau auf ein zugehöriges $y \in C$ ab und umgekehrt. - $enc: P \times K \rightarrow C$ bildet von einem Schlüssel und einem Klartext auf einen Ciphertext ab.
- $dec: C \times K \rightarrow P$ bildet von einem Schlüssel und einem Ciphertext auf einen Klartext ab.
Zu jedem Verschlüsselungsschlüssel $k_e \in K$ gibt es einen zugehörigen Entschlüsselungsschlüssel $k_d \in K$, sodass $x = dec(enc(x, k_e), k_d)$ für $x \in P$. Das bedeutet dec ist die inverse Operation für enc. Wenn mit $k_e$ verschlüsselt wurde kann nur der zugehörige $k_d$ verwendet werden, um den verschlüsselten Text wieder zu entschlüsseln.
Lässt sich der Schlüssel $k_e \in K$ aus dem zugehörigen Schlüssel $k_d \in K$ ableiten, so spricht man von einem symmetrischen Kryptosystem. Der triviale Fall ist dabei $k_e = k_d$. Ein Beispiel hierfür wäre der AES Cipher.
Ist es nicht möglich den Schlüssel $k_e \in K$ vom zugehörigen $k_d \in K$ abzuleiten, so spricht man von einem asymmetrischen Kryptosystem (nicht möglich bedeutet in diesen Fällen, dass es keinen Polynomialzeitalgorithmus gibt). Asymmetrische Kryptosysteme werden auch Public-Key-Kryptosysteme genannt, da $k_e$ als privater und $k_d$ als öffentlicher Schlüssel bezeichnet wird.
Da bei asymmetrischen Kryptosystemen $k_e$ nicht von $k_d$ abgeleitet werden kann und ein mit $k_d$ verschlüsselter Text nur mit dem zugehörigen $k_e$ wieder entschlüsselt werden kann ist es unkritisch, $k_d$ der Öffentlichkeit preiszugeben, daher auch der Name Public-key.
Beispiel RSA
RSA ist wohl eines der bekanntesten asymmetrischen Kryptosysteme. Es ist definiert als:
- $P = C = \mathbb{Z}_n$
- $K = \{ (n,p,q,e,d) \enspace | \enspace n = pq \enspace für \enspace p,q \enspace prim \enspace und \enspace ed \equiv 1 \enspace (mod \enspace \phi(n)) \}$
- $k_d = (n, e)$ (öffentlicher Schlüssel)
- $k_e = (p, q, d)$ (privater Schlüssel)
- $enc(k_d, x) = x^e \enspace (mod \enspace n)$
- $enc(k_e, y) = y^d \enspace (mod \enspace n)$
$\phi$ ist die eulersche Phi-Funktion, d.h. die Anzahl der Zahlen teilerfremd zu $n$ im Bereich $1 \le \phi(n) \lt n$. Formal: $\phi(n) = | \{ a \in \mathbb{N} : 1 \le a \le n \enspace und \enspace ggT(a, n) = 1\} | = | \mathbb{Z}^*_n |$
Der Schlüssel $k_d$ ist öffentlich und kann dazu genutzt werden eine verschlüsselte Nachricht an den Besitzer des zugehörigen $k_e$ zu senden, wobei $k_e$ geheimgehalten werden muss.
Verschlüsselung
Angenommen Bob möchte eine Nachricht $x$ an Alice schicken.
Zuerst sendet Alice den Schlüssel $k_d$, über einen sicheren Kanal (wie dies im Detail aussieht ist für den Moment irrelevant), an Bob. Bob verwendet den $k_d$ nun, um die Nachricht $x$ mittels der Funktion $enc$ zu verschlüsseln, d.h. $y = enc(k_d, x) = x^e \enspace (mod \enspace n)$. Nun sendet Bob die geheime Nachricht $y$ über einen möglicherweise unsicheren Kanal an Alice. Diese kann nun mit dem zugehörigen geheimen Schlüssel $k_e$ die Nachricht wieder entschlüsseln, d.h. $x = dec(k_e, y) = y^d \enspace (mod \enspace n)$.
Die Sicherheit von RSA basiert dabei auf dem Faktorisierungsproblem, d.h. es gibt keinen Polynomialzeitalgorithmus, mit dem sich $n$ (effizient) in seine Primfaktoren $p$ und $q$ zerlegen lässt. Weiterhin gibt es keinen effizienten Algorithmus, mit dem sich die Potenz $x^e \enspace mod \enspace n$ invertieren lässt, ohne die Primfaktoren $p,q$ zu kennen.
Das tolle an asymmetrischen Kryptosystemen ist, dass Alice auch eine mit $k_e$ verschlüsselte Nachricht an Bob schicken kann und sich daraus ganz neue Eigenschaften ergeben.
Digitale Signaturen
Wenn Alice eine mit $k_e$ verschlüsselte Nachricht an Bob schickt, so ist die Vertraulichkeit definitiv nicht gewährleistet, da potenziell jeder mit dem öffentlichen Schlüssel die Nachricht wieder entschlüsseln kann. Das bedeutet jedoch nicht, dass sich daraus kein Nutzen ergibt.
Wird eine Nachricht mit dem privaten Schlüssel verschlüsselt, so spricht man von einer digitalen Signatur, mit der die Authentizität (es kann nachvollzogen werden von wem die Nachricht stammt) und Integrität (die Nachricht kann nicht unbemerkt verändert werden) gewährleistet werden kann.
Dies kann man sich so überlegen: Nur Alice kennt den privaten Schlüssel $k_e$ und eine Nachricht die mit $k_e$ verschlüsselt wurde, kann nur mit dem zugehörigen $k_d$ entschlüsselt werden. Das bedeutet, wenn Bob die Nachricht erfolgreich entschlüsseln kann, kann er sich sicher sein, dass die Nachricht von Alice stammt. Weiterhin ist eine Anforderung an Kryptosysteme, über die noch nicht gesprochen wurde, dass selbst kleinste Änderungen am Text, beim ver-/ entschlüsseln zu völlig anderen Ausgaben führen. Damit ist es nicht ohne weiters möglich, den Text unbemerkt zu manipulieren.
Genau dieses Konzept, von digitalen Signaturen, macht sich FIDO2 für die Authentifizierung zu nutze, wobei nicht nur RSA sondern auch andere asymmetrische Kryptosysteme, wie z.B. ECDSA (ES256), zum Einsatz kommen.
Protokolle
Bei der Authentifizierung mittels FIDO2 sind drei Parteien involviert. Zum einen gibt es die Relying Party, bei welcher es sich um den Server/ die Anwendung handelt, gegenüber welcher man sich authentifizieren möchte. Dann gibt es den Client, oder auch Host genannt, der sich authentifizieren möchte und schlussendlich den Authenticator selber. Bei diesem kann es sich um dedizierte Hardware handeln (YubiKey, Solo1) oder um eine Anwendung, die im Client integriert ist (Windows Hello). Bei dedizierter Hardware spricht man dann von Roaming- und beim Rest von Platform-Authenticatoren.
Da drei Parteien involviert sind, gliedert sich FIDO2 in zwei Protokolle. Das erste Protokoll regelt die Kommunikation zwischen Relying Party und Client und wird als Web Authenticatorion (kurz WebAuthn) bezeichnet. Das zweit Protokoll regelt die Kommunikation zwischen Client und Authenticator und wird als Client to Authenticator Protocol (CTAP2) bezeichnet.
Die zwei wichtigsten Funktionen von WebAuthn und CTAP2 sind das Erstellen neuer Credentials (Registrierung) und das Erstellen von Assertions (Authentifizierung).
Registrierung
Bei der Registrierung wählt der Nutzer im Regelfall einen Nutzernamen bzw. gibt seine E-Mail Adresse an. Die Relying Party sendet dann Informationen über sich, den Nutzer, eine Challenge (zufällig generierte Zahl) und eine Liste unterstützter Cipher Suits an den Client, welcher einen Teil der Daten hashed (clientDataHash) und alles an den Authenticator weiterleitet.
Der Authenticator wählt dann eine der gegebenen Cipher Suits aus und generiert ein neues Schlüsselpaar (Credential), welches an den Nutzer und die Relying Party (rpId: normalerweise die Basis-URL wie z.B. https://fidoalliance.org/) gebunden wird. Dies geschieht jedoch erst, nachdem der Nutzer noch einmal physisch (z.B. durch Knopfdruck) bestätigt hat, dass er die Operation auch durchführen möchte, was als User Presence (up) bezeichnet wird.
Schlussendlich wird der öffentliche Schlüssel, über den Client, an die Relying Party geschickt, welche diesen speichert. Der private Schlüssel verbleibt geschützt auf dem Authenticator.
Wichtig: Viele Details wurden in dieser knappen Zusammenfassung unterschlagen. Darunter fällt z.B. wie der öffentliche Schlüssel sicher übermittelt werden kann, da ohne Schutzvorkehrungen ein Man-in-the-Middle Angriff möglich ist.
Authentifizierung
Wenn sich ein Nutzer authentifizieren möchte (z.B. beim Login) schickt die Relying Party ihre ID, eine Challenge und weitere Daten an den Client. Dieser leitet die ID und einen Hash der Daten (clientDataHash) an den Authenticator weiter.
Der Authenticator überprüft, nachdem die User Presence festgestellt wurde, ob ein passender privater Schlüssel auf dem Authenticator hinterlegt ist und signiert mit diesem den clientDataHash. Die Signatur wird danach zurück an die Relying Party gesendet, welche die Signatur überprüft. Sollte die Signatur korrekt sein, so hat sich der Nutzer erfolgreich authentifiziert.
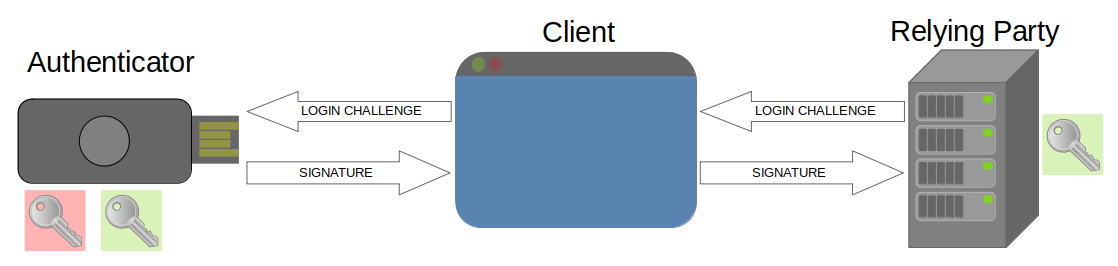
Wichtig: Auch hier werden viele Details unterschlagen.
Vorteile von FIDO2
FIDO2 ist nicht perfekt, bietet aber einige Vorteile gegenüber Passwörter, sowie klassischen Zwei-Faktor-Authentifizierungsmethoden.
- Unter der Voraussetzung, dass der öffentliche Schlüssel $k_d$, während des Registrierungsprozesses, erfolgreich und sicher an die Relying Party übermittelt wurde, ist eine Man-in-the-Middle Angriff aussichtslos, solange der $k_e$ geheim bleibt.
- Außerdem sollten Phishing-Seiten schnell auffallen, da jeder Credential an die jeweilige URL der Relying Party gebunden ist.
- Weiterhin haben Datenpannen kein Auswirkung auf die Sicherheit der Authentifizierung, da ein Angreifer mit dem $k_d$ höchstens geheime Nachrichten an den Authenticator schicken kann.
- Digitale Signaturen sind, solange richtig implementiert, sicher.
Nachteile von FIDO2
- Ein großer nachteil ist, dass es bisher keine bequeme Möglichkeit gibt seinen Authenticator auf allen verwendeten Webseiten zu sperren, sollte dieser z.B. verloren gehen.
- Außerdem ist es nicht zwingen notwendig eine PIN zu vergeben, d.h. sollte eine unberechtigte Person Zugang zu einem Authenticator erhalten, so kann sich diese ungehindert bei jeder RP anmelden, bei der der gegebene Authenticator registriert ist.
Zusammenfassung
FIDO2 ist nicht das Allerheilmittel, jedoch hat FIDO2 das Potenzial die Angriffsfläche von Unternehmen und Privatpersonen deutlich zu verkleinern. Es bleibt abzuwarten, wann der Standard endlich in den Mainstream vordringt.
Ich hoffe diese kurze Zusammenfassung war hilfreich. Bei Fragen und Anregungen erreicht man mich unter david(at)thesugar.de. Grundsätzlich plane ich aus diesem Beitrag eine Serie zu machen und verschiedene Aspekte von FIDO2 näher zu beleuchten. Bis es soweit ist… Happy Hacking.
